Die Physik um 1877
Einleitung
Prof. Jolly an der Uni München rät Planck ab, sich mit Theoretischer Physik zu befassen. Er sagte, laut Planck: „Die Theoretische Physik nähert sich der Vollendung, die etwa die Geometrie seit Jahrhunderten erreicht hat.“ „Wohl gäbe es vielleicht in einem oder dem anderen Winkel noch ein Stäubchen oder ein Bläschen zu prüfen und einzuordnen“, aber das System als Ganzes stehe ziemlich gesichert da.

Die Physik um 1877
Einleitung
Die Physik bestand damals aus drei Teilgebieten: Elektrodynamik, Thermodynamik und Mechanik, wobei letztere „über allen thronte“, nicht zuletzte durch die Autorität Isaac Newtons.
Zwei „Stäubchen“ (offene Fragen) sind angedeutet, die damals allerdings niemand als schwerwiegendes Problem angesehen hatte.
Das erwies sich als ein gewaltiger Irrtum: Aus dem Problem der Strahlung bewegter Körper entwickelte sich 1905 Einsteins Relativitätstheorie, und aus dem Problem der Wärmestrahlung 1900 die Plancksche Quantentheorie und bald darauf die Quantenmechanik. Bereits 30 Jahre später hatte die Physik eine vollständige Umwälzung erfahren.

Modell des Schwarzen Körpers
Wärmestrahlung oder Hohlraumstrahlung
1860 formuliert Gustav Kirchhoff das Modell eines Körpers, in dem Licht „eingesperrt“ ist und immer wieder reflektiert wird „Schwarzer Körper“.
Entscheidend für das Gedankenexperiment:
Das Licht befindet sich im Thermodynamischen Gleichgewicht. Es hat also genug Zeit, eine stabile Energieverteilung über die verschiedenen Frequenzen (Farben) zu erreichen. Diese Verteilung galt es zu finden.

1860 formuliert Gustav Kirchhoff das Modell eines Körpers, in dem Licht „eingesperrt“ ist und immer wieder reflektiert wird „Schwarzer Körper“.
Entscheidend für das Gedankenexperiment:
Das Licht befindet sich im Thermodynamischen Gleichgewicht. Es hat also genug Zeit, eine stabile Energieverteilung über die verschiedenen Frequenzen (Farben) zu erreichen. Diese Verteilung galt es zu finden.

Wiensches Verschiebungsgesetz
Einleitung
Wilhelm Wien findet heraus, dass die Strahlungskurve unabhängig vom Material ist und nur von der Temperatur abhängt. Die Frequenz, bei der die Kurve ihr Maximum besitzt, ist umgekehrt proportional zur Temperatur des Körpers (in Kelvin).

Wilhelm Wien findet heraus, dass die Strahlungskurve unabhängig vom Material ist und nur von der Temperatur abhängt. Die Frequenz, bei der die Kurve ihr Maximum besitzt, ist umgekehrt proportional zur Temperatur des Körpers (in Kelvin).

Plancks Entdeckung
Planck-Konstante h
Max Planck führte diese Größe 1899 ein und gab die ZIffern h= 6.885 an, die bereits erstaunlich nah am heutigen Wert sind. Das Wirkungsquantum wurde 2019 auf den Wert h= festgelegt und bildet die Grundlage des neuen internationalen Einheitensystems.

Das PTR-Versuchslabor
Einleitung

Während die Theoretiker versuchen, das Strahlungsgesetz zu finden, das sie Messwerte in allen Wellenlängenbereichen wiedergibt, besteht die Herausforderung der Experimentalphysiker darin, einen möglichst idealen Schwarzen Körper herzustellen und dessen Spektrum (d.h. die Verteilung der Wellenlängen des emittierten Lichts) genau zu vermessen.
Das PTR-Versuchslabor
Die Wissenschaftler

Ernst Pringsheim
Wie Lummer proviert auch Pringsheim bei Helmholtz an der Friedrich-Wilhelms-Universität in Berlin. Er beschäftigt sich mit der Messung von Wellenlängen im infraroten Bereich des Sonnenspektrums und arbeitet ab 1896 mit Lummer an der PTR.

Heinrich Rubens
Er wird 1896 als Ordinarius an die Technische Hochschule Berlin berufen.
Da seine Forschungsmöglichkeiten dort sehr begrenzt sind, ist er als offizieller Gast an der PTR tätig. Zusammen mit Kurlbaum führt er außerordentlich präzise Messungrn zur Schwarzkörperstrahlung durch, die im Bereich des äußersten Ultrarot gravierende Abweichungen von der wienschen Strahlungsformel erkennen ließen.

Ferdinand Kurlbaum
Er ist ein weiterer Helmholtz-Schüler. Seine Dissertattion (1887) befasst sich mit der Präzisionsbestimmung der Wellenlänge von Fraunhoferlinien im Sonnenspektrum. Er ist ab 1891 an der PTR und wird 1904 Professor an der Technischen Hochschule Berlin.

Otto Richard Lummer
Otto Richard Lummer. Er promoviert 1884 bei Heimholtz und wird 1887 wissenschaftlicher Mitarbeiter in der gerade gegründeten Physikalisch-Technischen Reichsanstalt. Seine besondere Begabung liegt in der Konstruktion neuer Messapparaturen.
Das PTR-Versuchslabor
Die Messergebnisse
Strahlungsleistung als Funktion der Wellenlänge (in Mikrometern, x-Achse) für eine fixierte Temperatur von T= 1650 Grad Kelvin. Das Bild zeigt drei Kurven, die insgesamt sehr gut übereinstimmen. Abweichungen fanden Lummer und Pringsheim 1899-1900 in neuen Messungen bei großen Wellenlängen.
Diese Abweichung war der Auslöser für Plancks Untersuchung und Entdeckung: Plancks Strahlungsgesetz deckt sich mit der experimentellen Kurve.
Plancks Entdeckung
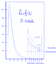
Plancksches Strahlungsgestz
Das plancksche Strahlungsgetz beschreibt das Spektrum des Schwarzen Körpers, das heißt die Verteilung der Strahlungsenergie auf die verschiedenen Frequenzen (Farben) der Strahlung in Abhängigkeit von der Temperatur des Schwarzen Körpers. Das Gesetz ist für beliebige strahlende Körper gültig.